|
|
Sequência didática |
Expressões algébricas, equações e sistemas de equações
Nesta sequência didática, serão trabalhadas expressões algébricas, equações de 1º e 2º grau e, ainda, sistemas de equações de 1º grau com duas incógnitas.
A BNCC na sala de aula
|
Objetos de conhecimento |
Valor numérico de expressões algébricas. Associação de uma equação linear de 1º grau a uma reta no plano cartesiano. Sistema de equações polinomiais de 1º grau: resolução algébrica e representação no plano cartesiano. Equação polinomial de 2º grau do tipo ax² = b. |
|
Competências específicas |
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes. 5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados. |
|
Habilidades |
(EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações. (EF08MA07) Associar uma equação linear de 1º grau com duas incógnitas a uma reta no plano cartesiano. (EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso. (EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2º grau do tipo ax² = b. |
|
Objetivos de aprendizagem |
Escrever expressões algébricas. Calcular o valor numérico de uma expressão algébrica. Representar as soluções de uma equação de 1ºgrau com duas incógnitas no plano cartesiano. Resolver sistemas de equações de 1º grau com duas incógnitas. Resolver equações polinomiais de 2º grau do tipo ax² = b. |
|
Conteúdos |
Expressões algébricas. Equações de 1º grau com duas incógnitas. Sistemas de equações de 1º grau com duas incógnitas. Equações polinomiais de 2º grau. |
Materiais e recursos
Canetinha colorida.
Folhas de papel sulfite.
Software de geometria dinâmica.
Desenvolvimento
Quantidade de aulas: 5.
Aula 1
Nesta aula, os alunos deverão escrever expressões algébricas para representar determinadas situações. Para tanto, iniciar a aula solicitando que cada aluno escolha um número de 1 a 40 e o anote no caderno, utilizando uma caneta colorida ou contornando esse número para destacá-lo. Em seguida, solicitar que calculem o dobro desse número e registrem o resultado. Orientá-los a organizar os valores registrados conforme apresentado a seguir, por exemplo.

Elaborado pelo autor.
Exemplo de registro pelo aluno.
Cada aluno poderá obter um resultado diferente de outro, dependendo do número que escolheram. Questioná-los sobre o que diriam caso entrasse na sala de aula um novo aluno e lhes perguntassem o que fizeram. Espera-se que eles respondam que escolheram um número e calcularam o dobro desse número, ou seja, multiplicaram o número escolhido por dois.
Explicar que o número a ser escolhido pelos alunos pode ser representado pela letra x e para calcular o dobro desse número é preciso multiplicá-lo por 2. Assim, solicitar aos alunos que registrem essa informação no caderno com as anotações que realizaram anteriormente, utilizando uma expressão algébrica, conforme exemplo a seguir.

Elaborado pelo autor.
Exemplo de registro pelo aluno.
Agora, propor aos alunos que calculem a metade do número que escolheram e registrem o resultado. Depois, solicitar que escrevam uma fração para representar essa divisão considerando um número escolhido qualquer (x).
Propor aos alunos que realizem outros cálculos, como os sugeridos a seguir, e registrem os resultados.
O triplo de um número.
O dobro de um número mais 5.
Um número menos 10.
Um número subtraído de 20.
O dobro de um número menos 100.
Em seguida, apresentar a expressão algébrica 2x + 5 e dizer aos alunos que sua leitura pode ser realizada como "o dobro de um número mais 5" ou "dois x mais 5", por exemplo. Perguntar a eles qual o valor numérico dessa expressão se x for igual a 2? Nesse momento, espera-se que os alunos realizem os cálculos mentalmente, mas é importante verificar se o cálculo que efetuaram é 2 · 2 + 5, obtendo 9 como resultado.
Propor aos alunos algumas atividades, como as sugeridas a seguir.
1. Uma confeiteira produz 120 brigadeiros por hora de trabalho.
a) Quantos brigadeiros ela produz em duas horas?
240 brigadeiros.
b) Quantos brigadeiros ela produz em cinco horas?
600 brigadeiros.
c) Quantos brigadeiros ela produz em x horas?
120x brigadeiros.
2. Associe cada expressão algébrica a seguir ao seu valor numérico para x = 2. Para isso, escreva a letra e o símbolo romano correspondente.
A-III; B-I; C-V; D-II; E-VI; F-IV
|
A) 3x – 2 |
I) –4 |
|
B) –2x |
II) –2 |
|
C) |
III) 4 |
|
D) |
IV) –3 |
|
E) |
V) 1 |
|
F) |
VI) 2 |
Após os alunos resolverem as atividades, solicitar que alguns deles apresentem para o restante da turma as estratégias que utilizaram.
Para finalizar, solicitar que escrevam em uma folha de papel sulfite uma expressão algébrica para representar o dobro de um número, o triplo e a metade desse número.
Aula 2
Iniciar a aula organizando os alunos em duplas. Perguntar se eles já viram ou sabem como funciona uma balança de dois pratos. Comentar que, muito antes do surgimento das modernas balanças digitais, esse tipo de balança era muito utilizado pelos comerciantes para realizar pesagens por meio de comparação e obter, por exemplo, 1 kg de batata. Explicar que, em um dos pratos, colocava-se o que se queria medir a massa e, no outro, pequenas peças de metal com massas variadas conhecidas. A balança equilibrada indicava que a massa nos dois pratos era a mesma.
Desenhar na lousa um esquema que represente uma balança de dois pratos em equilíbrio contendo algumas caixas e uma peça de metal com sua massa indicada. Observe a seguir um exemplo.
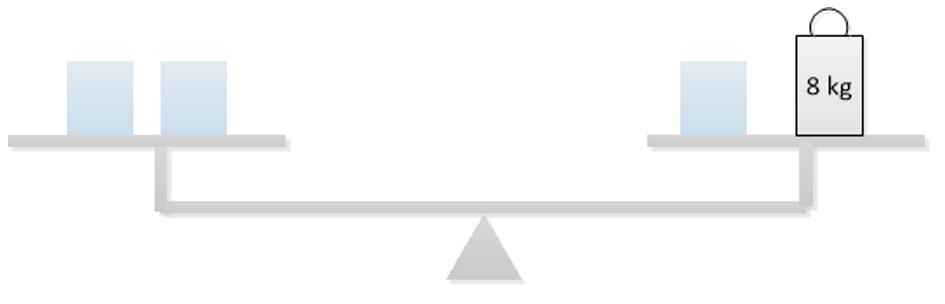
Elaborado pelo autor.
Balança em equilíbrio.
Explicar que todas as caixas possuem a mesma massa e que, se retirarmos a mesma quantidade de caixas, dos dois pratos da balança, essa permanecerá em equilíbrio.
Em seguida, solicitar aos alunos que determinem a massa de cada caixa. Convidar um aluno para explicar ao restante da turma como fez para determinar essa massa.
Dizer aos alunos para considerarem que x representa a massa de cada caixa e solicitar que escrevam uma equação para representar a situação apresentada. Nesse momento, convidar alguns alunos para explicar como pensaram. Resolver a equação com os alunos e realizar a verificação do resultado obtido, substituindo a incógnita na equação pelo valor desse resultado.
Propor aos alunos que resolvam as atividades a seguir. Para isso, reproduzir os enunciados dessas atividades e distribuir uma cópia para cada dupla, com algumas folhas de papel sulfite. Enquanto os alunos resolvem as atividades, circular pela sala de aula procurando identificar as estratégias utilizadas por eles e, quando necessário, direcionando-os a utilizar outras estratégias.
1. As balanças representadas a seguir estão em equilíbrio e as caixas de mesma cor têm massas iguais. Determine a massa de cada caixa que está sem marcação.
a)
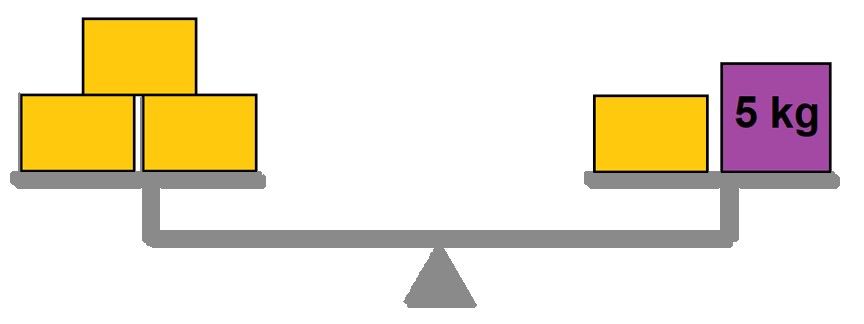
Caixa alaranjada: 2,5 kg.
b)
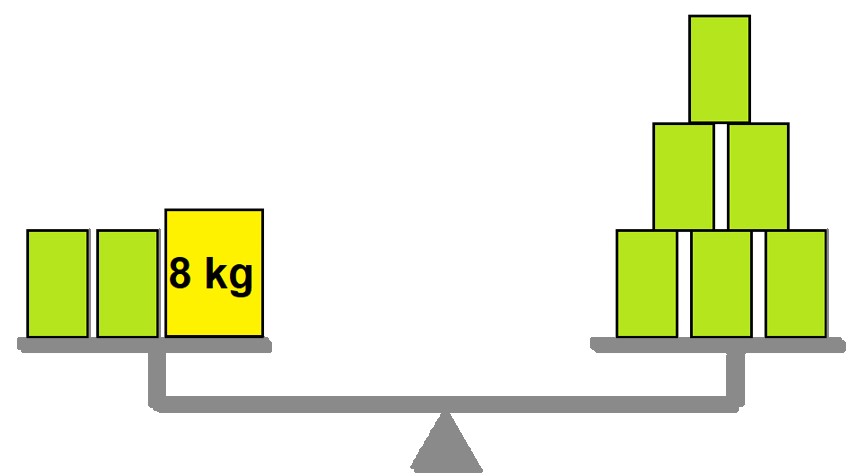
Caixa verde: 2 kg.
c)
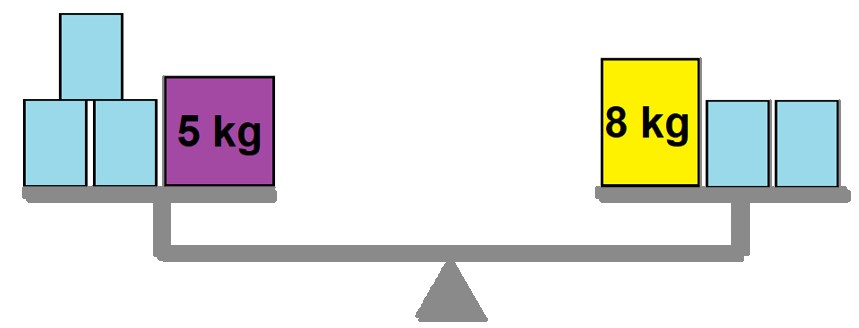
Elaborado pelo autor.
Caixa azul: 3 kg.
2. A balança representada a seguir está em equilíbrio e as caixas verdes têm todas massas iguais. Escreva uma equação para representar a pesagem realizada por essa balança. Em seguida, resolva essa equação.
5x + 6 = 4x + 9, em que x representa a massa da caixa verde; x = 3
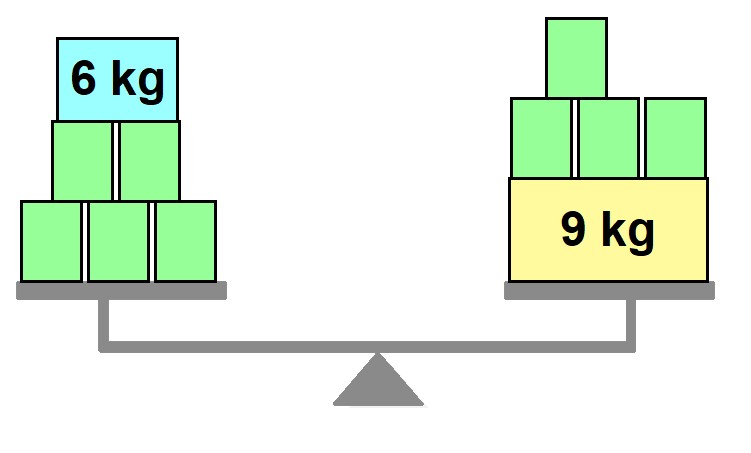
Elaborado pelo autor.
3. As balanças representadas a seguir estão em equilíbrio e nelas foram colocadas algumas caixas. Sabendo que as caixas de mesma cor têm massas iguais, determine a massa de cada caixa amarela e cada caixa azul.
Caixa amarela: 3 kg; caixa azul: 6 kg
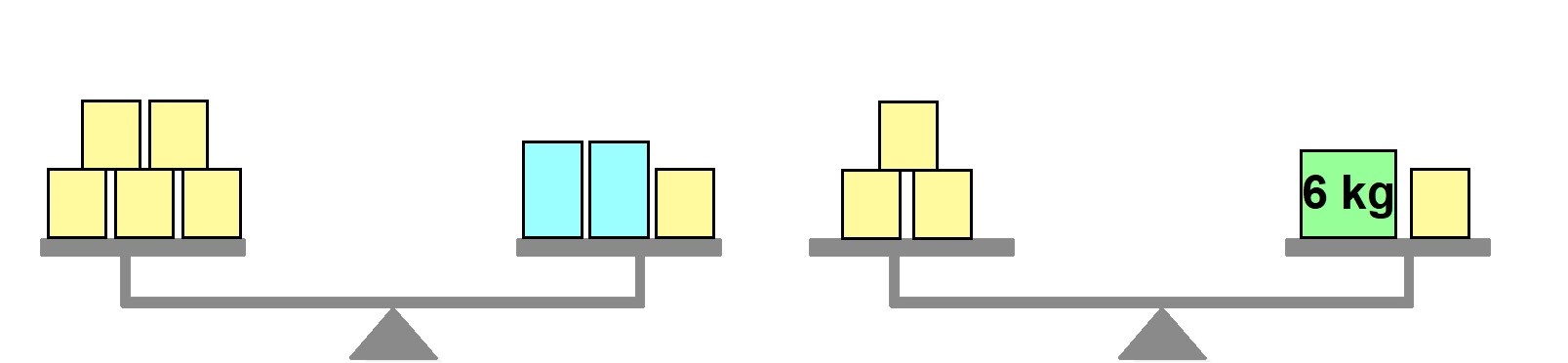
Elaborado pelo autor.
Verificar se os integrantes de cada dupla discutem entre si as estratégias para resolver cada atividade. Verificar também se eles perceberam, na atividade 3, a necessidade de obter a massa da caixa amarela em uma balança para, depois, obter a massa da caixa azul na outra balança.
Realizar a correção dessas atividades na lousa com os alunos e aproveitar a discussão sobre a atividade 3 para explicar que, nesse caso, como há duas massas desconhecidas, a massa da caixa amarela e a massa da caixa azul, pode-se utilizar uma letra para representar a massa de cada uma delas e escrever uma equação para representar a pesagem em cada balança.
Em seguida, propor aos alunos mais algumas atividades, como as sugeridas a seguir.
4. Em relação à situação apresentada na atividade anterior, considere a massa de cada caixa amarela igual a x e a massa de cada caixa azul igual a y. Escreva uma equação para representar a pesagem em cada balança.
5x = 2y + x; 3x = 6 + x
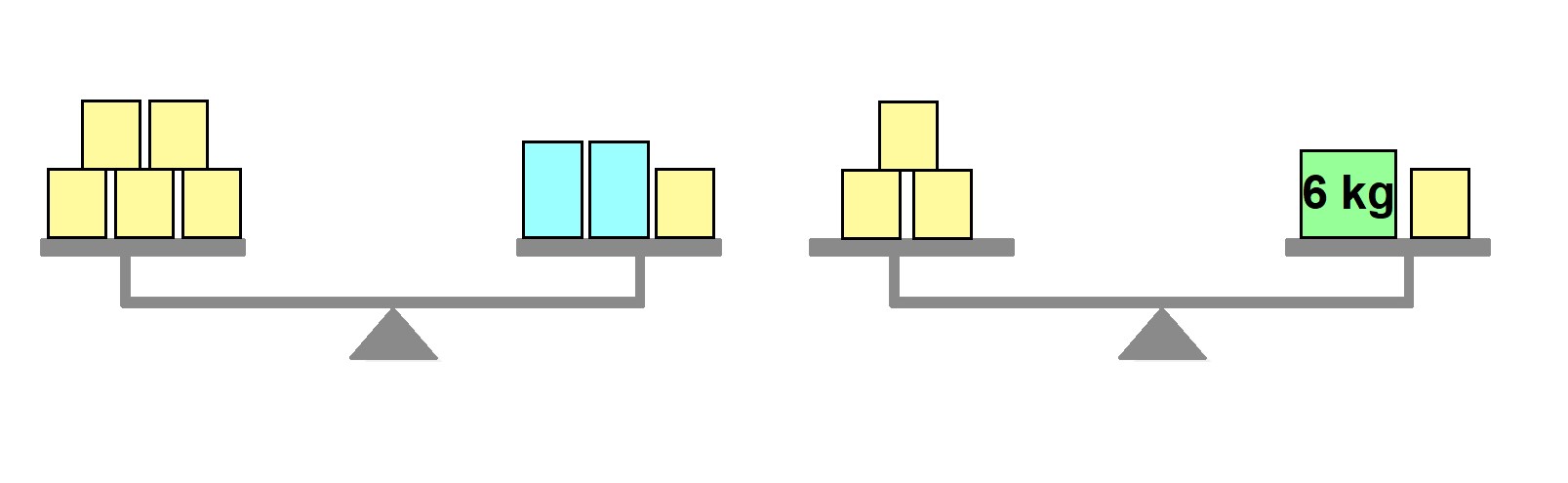
Elaborado pelo autor.
5. As balanças representas a seguir estão em equilíbrio e as caixas de mesma cor têm massas iguais.

Elaborado pelo autor.
a) Compare as duas balanças e determine a massa de cada caixa alaranjada e de cada caixa roxa.
Caixa alaranjada: 4 kg; caixa roxa: 2 kg.
b) Escreva um sistema com duas equações, de maneira que cada equação represente a pesagem de cada uma das balanças. Em seguida, resolva o sistema e compare com a resposta do item anterior.
, em que x representa a massa da caixa alaranjada e y a massa da caixa roxa.
Após todas as duplas resolverem essas atividades, solicitar que algumas delas apresentem suas resoluções para o restante da turma.
Aulas 3 e 4
Agendar com antecedência para que estas aulas sejam realizadas no laboratório de informática da escola. Verificar se há algum software de geometria dinâmica instalado nos computadores ou solicitar que sejam instalados.
Iniciar a aula organizando os alunos em duplas e relembrando com eles o que foi trabalhado nas aulas anteriores. Explicar que nem sempre é possível registrar em uma folha de papel todas as soluções de uma equação. Para apresentar um exemplo, perguntar a eles quais dois números que, se adicionados, resulta em 16. É importante ressaltar que, além das soluções que envolvem apenas números naturais, existem também as soluções que envolvem números inteiros e racionais.
Listar algumas das possibilidades de solução a fim de que os alunos percebam que existem infinitos pares de números que, adicionados, resultam em 16, ou seja, representando essa situação pela equação x + y = 16, em que x e y representam os números a serem adicionados, dizemos que essa equação possui infinitas soluções. Explicar então que podemos representar as soluções de uma equação desse tipo, com duas incógnitas, por uma reta em um plano cartesiano e que eles realizarão algumas dessas representações utilizando um software de geometria dinâmica.
Assim, solicitar que utilizem o software e digitem a equação x + y = 16 para obterem uma reta representada no plano cartesiano. Explicar aos alunos que as coordenadas de todos os pontos pertencentes à essa reta, representam uma solução da equação x + y = 16. Dessa maneira, como a reta não passa pelo ponto de coordenadas (15, 0), por exemplo, temos que x = 15 e y = 0 não é uma solução da equação. Da mesma maneira, como a reta passa pelo ponto de coordenadas (0, 16), por exemplo, temos que x = 0 e y = 16 é uma solução da equação.
Propor aos alunos que, em duplas, explorem as ferramentas do software. Em seguida, propor que realizem as atividades a seguir utilizando o software.
1. Represente as soluções de cada equação a seguir.
a) x + y = 10
b) x – y = 4.
c) x = 2y
d) –x – y = 1
e) –x + y = 6
Resposta:
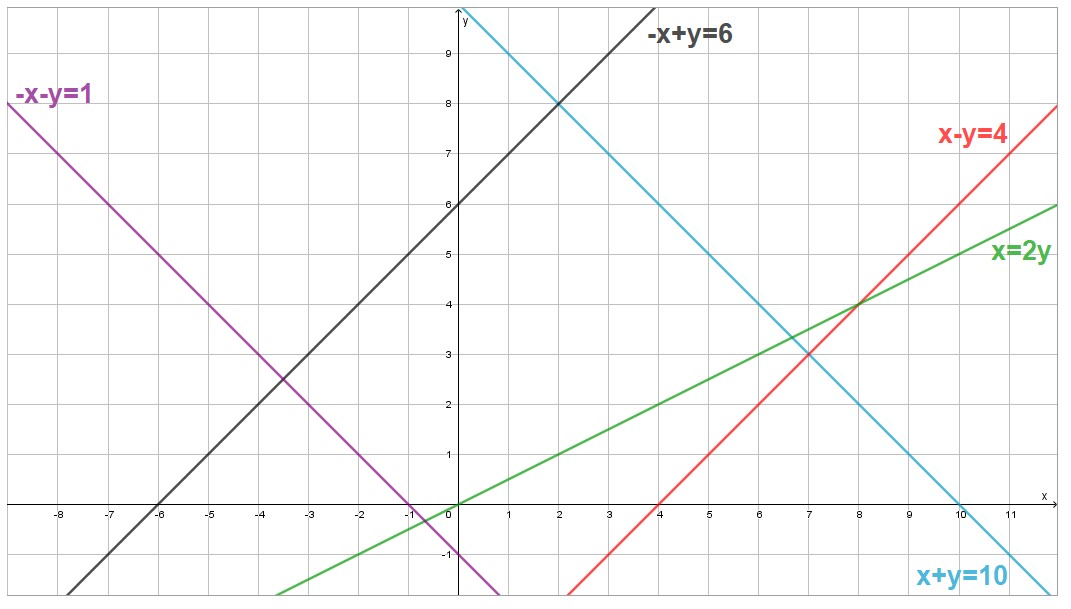
Elaborado pelo autor.
2. Considere as equações x + y = 4 e x – y = 4. Elas têm alguma solução em comum? Justifique.
Resposta esperada: Sim, pois ao representar as soluções das duas equações por retas no plano cartesiano temos que o ponto de coordenadas (4, 0) pertence às duas retas.
Explicar aos alunos que também é possível resolver um sistema de equações com auxílio do mesmo software. Para isso, é preciso representar as duas equações que compõem o sistema em um mesmo plano cartesiano e verificar os pontos que essas restas possuem em comum.
Propor aos alunos que determinem as soluções dos sistemas de equações a seguir com auxílio do software.
(5, 1)
(4, –2)
(–1,1)
Não tem solução.
Possui infinitas soluções.
Possui infinitas soluções.
Não tem solução.
Verificar se os alunos perceberam que alguns pares de retas têm apenas um ponto em comum, infinitos pontos em comum e nenhum ponto em comum. Dizer que isso ocorre quando as retas que representam as soluções de cada equação de um sistema de equações de 1º grau são, respectivamente, concorrentes e não coincidentes, coincidentes e paralelas entre si.
Em seguida, propor aos alunos que resolvam algumas atividades, como as sugeridas a seguir com auxílio do software de geometria dinâmica.
1. Observe as representações de dois terrenos retangulares. Sabendo que o perímetro do Terreno I é de 140 m e do Terreno II é de 160 m, determine as dimensões de cada terreno.
Terreno I: 30 m de largura e 40 m de comprimento; terreno II: 20 m de largura de 60 m de comprimento.
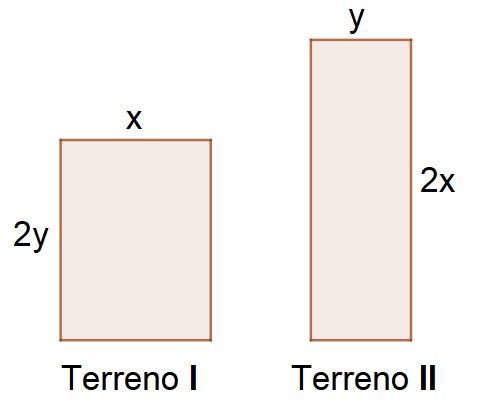
Elaborado pelo autor.
2. Uma loja de decoração preparou uma seguinte promoção de maneira que:
O cliente que comprar 2 banquetas e 3 tapetes pagará R$ 510,00.
O cliente que comprar 3 banquetas e 2 tapetes pagará R$ 465,00.
De acordo com essas informações, quanto custa um tapete?
R$ 120,00
Para finalizar a aula, promover uma roda de conversa a fim de que os alunos relatem as principais conclusões das atividades que realizam nessas aulas.
Aula 5
Espera-se que, ao final desta aula, os alunos constatem que as equações de 2º grau podem admitir duas raízes reais e distintas.
Iniciar a aula organizando os alunos em duplas. Escrever na lousa o enunciado da seguinte situação:
Três quadrados congruentes foram desenhados lado a lado, formando um retângulo de 27 cm² de área. Quanto mede o lado de cada quadrado?
Espera-se que os alunos determinem a área de cada quadrado (9 cm²) e, na sequência, a medida do lado desses quadrados (3 cm).
Conceder um tempo para que os alunos possam resolver o problema e, em seguida, solicitar que algumas duplas expliquem como fizeram para determinar a medida do lado do quadrado. Dizer a eles que a situação apresentada pode ser representada por meio de uma equação de 2º grau (3x² = 27).
Depois, propor a seguinte questão: "O dobro do quadrado de um número é igual a 50. Que número é esse?". Deixar que os alunos pensem um pouco a respeito dessa questão e apresentem suas respostas. Eles podem determinar as raízes (5 e –5) dessa equação por meio de tentativas.
Escrever na lousa, com os alunos, a seguinte equação para representar a situação apresentada: 2x² = 50. Dizer a eles que se trata de uma equação de 2º grau com uma incógnita e que essa equação pode ser resolvida da seguinte maneira:
ou
ou
Assim, essa a equação 2x² = 50 possui duas raízes.
Propor mais algumas atividades, como as sugeridas a seguir, para os alunos e solicitar que registrem os cálculos e estratégias que utilizarem em suas resoluções.
1. Gabriela está reformando seu apartamento e, para colocar em uma janela, utilizará 21 peças de vidro de formato retangular de dois tamanhos diferentes: 600 cm² e 1 000 cm². Sabendo que essas peças deverão cobrir uma área total de 15 400 cm², quantas peças de vidro de cada tamanho serão utilizadas?
Serão utilizadas 14 peças de vidro de 600 cm² e 7 peças de vidros de 1 000 cm².
2. A soma de dois números é igual a 3 000. Quais são esses números sabendo que a metade do menor número entre eles subtraída do maior é igual a 1 491?
1 994 e 1 006.
Para finalizar a aula, realizar uma correção com os alunos na lousa. Nesse momento, é interessante retomar com os alunos os conceitos estudados.
Para trabalhar dúvidas
Verificar se os alunos apresentam dificuldades na escrita das expressões algébricas que envolvem o dobro e a metade de um número. Caso julgar necessário, apresentar alguns exemplos realizando a substituição das variáveis por números.
Em relação à resolução de equações envolvendo balança de dois pratos, verificar se eles compreenderam que para a balança se manter equilibrada, é preciso adicionar ou retirar uma mesma massa em ambos os pratos. Utilizando esse mesmo raciocínio, ao resolver uma equação deve-se multiplicar, por exemplo, ambos os membros por um mesmo número, a fim de manter a igualdade verdadeira.
Em relação à resolução de sistemas de equações de 1º grau com duas incógnitas, retomar a resolução de uma equação de 1º grau com uma ou duas incógnitas e como determinar a solução desse sistema.
Avaliação
Observar se os alunos conseguiram escrever expressões algébricas e determinar seu valor numérico, resolver equações de 1º grau e sistemas de equações de 1º grau com duas incógnitas, bem como se conseguiram reconhecer quando um sistema não possui solução, quando possui uma única solução ou quando possui infinitas soluções.
Verificar também se os alunos compreenderam como resolver uma equação de 2º grau do tipo ax² = b.
Para verificar se os alunos compreenderam e assimilaram as ideias trabalhadas nas aulas propostas nesta sequência didática, propor algumas atividades, como as sugeridas a seguir.
1. Em cada item, escreva uma expressão algébrica para representar a situação apresentada.
a) A adição entre um número e 100.
x + 100
b) A adição entre o dobro de um número e 4.
2x + 4
c) A metade de um número menos o triplo desse número.
d) 4 subtraído do quadrado de um número.
x² – 4
2. Determine o valor numérico da expressão algébrica x² + 2y – 10 para:
a) x = 2 e y = 5
4
b) x = –2 e y = –1
–8
c) x = 0 e y = –5
–20
3. Resolva os sistemas de equações.
a)
x = 4 e y = 3
b)
x = –4 e y = 3
c)
x = 3 e y = –4
Ampliação
É importante que os alunos tentem resolver um mesmo problema de diferentes maneiras. Para trabalhar essa ideia, organizar os alunos em pequenos grupos e propor alguns problemas que podem ser resolvidos de diferentes maneiras, como o sugerido a seguir.
Em um estacionamento há automóveis e motocicletas, totalizando 28 unidades e 88 rodas. Desconsiderando possíveis estepes, quantos automóveis e quantas motocicletas há nesse estacionamento?
